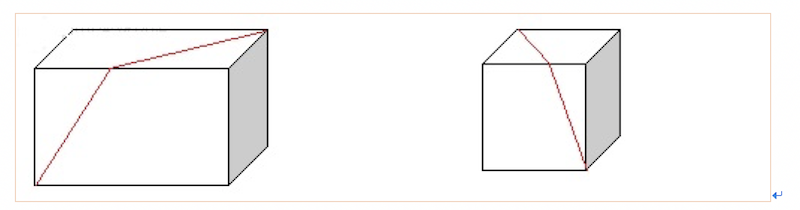
一天小Y由于打游戏不理女朋友导致被女朋友惩罚，要求他站在长方体的一个顶点，从这个顶点走到对立的另一个顶点，可是小Y只知道长方体里最长的那条边的边长，小Y很懒，如果要走到对立的另一个顶点他一定会选择最短的路线来走，假设这条路线是L，小Y想知道所有的可能性的L²的和，注意（4,5,6）和（6,5,4）属于同一种情况的长方体，

输入一个T作为组数，（T<=1000）,对每组输入一个n（1<=n<=10¹⁴）,代表了长方体里最长边的边长。

对每组数据，输出所有可能的L²的和，答案可能会很大，请把答案对1000000007取模。

用到的公式给出：

1³+2³+3³+4³+5³+。。。。+n³= [n(n+1)/2]²

1²+2²+3²+...+n²=n(n+1)(2n+1)/6.

Tip:给出逆元函数代码：

/*

typedef long long ll;

const ll mod=1000000007;

ll my_pow(ll ds,ll cf)

{

   ll sum=1;

   while(cf>0)

    {

       if(cf%2==1)

           sum=(sum*ds)%mod;

       ds=(ds*ds)%mod;

       cf/=2;

    }

   return sum;

}

ll inv(ll x)

{

   return my_pow(x,mod-2);

}

*/

(a/b) mod c =a*inv(b).

(a * b) mod c =((a mod c)* (b mod c)) mod c
mod 代表取模。